演繹的推論の変形

演繹的推論は既に証明されている事実（大前提）から、大前提の含まれている条件を満たしていることを述べ （小前提）、結論が正しいことを証明できる方法

では小前提が真ではなく偽（反対）の場合は、何が言えるのだろうか。結論も偽といえるのだろうか？
現実ではこのような判断の対処を求められることが多い。組み合わせには４つのパターンが存在する。それぞれに ついて正しいかを考えてみよう。

４つのパターンとは（大前提は変えない）

1. 小前提が真ならば、結論も真である
2. 結論が真ならば、小前提も真である
3. 小前提が偽ならば、結論も偽である
4. 結論が偽ならば、小前提も偽である

論法１

（大前提）もしもＡが真ならばＢは真である
（小前提）Ａは真
（結論）したがってＢは真

これは基本の演繹法であるので、正しい。

【例】
（大前提）もしも図形が3角形であるなら、赤い色をしている
（小前提）図形は3角形である
（結論）色は赤い

論法２

（大前提）もしもＡが真ならばＢは真である
（小前提）Ｂは真
（結論）したがってＡは真

これは正しくありません。Ａが真でなくともＢが真はあるのです

【例】
（大前提）もしも図形が3角形であるなら、赤い色をしている
（小前提）色は赤い
（結論）図形は3角形である

論法３

（大前提）もしもＡが真ならばＢは真である
（小前提）Ａは真ではない
（結論）したがってＢも真ではない

これは正しくありません。Ａが真でなくともＢが真はあるのです

【例】
（大前提）もしも図形が3角形であるなら、赤い色をしている
（小前提）図形は3角形ではない
（結論）色は赤ではない

論法４

（大前提）もしもＡが真ならばＢは真である
（小前提）Ｂは真ではない
（結論）したがってＡは真ではない

これは正しい：3角形であるなら赤い色をしているはず

【例】
（大前提）もしも図形が3角形であるなら、赤い色をしている
（小前提）色は赤ではない
（結論）図形は3角形ではない

ヴェン図で表すと分かりやすくなります

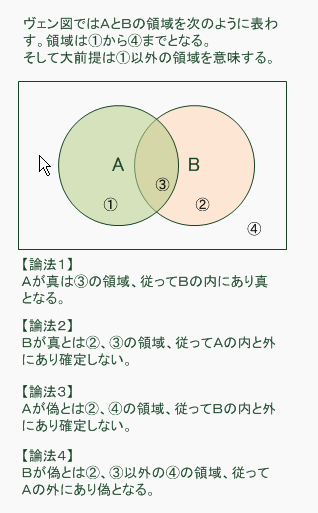
（この項終わり）